5 估计贸易方程
四个方程 (16)、(17)、(20)、(21) 构成了一个一般均衡模型,决定了价格水平、贸易份额、制造业工资(劳动力不可跨部门流动)或者制造业就业(劳动力可以跨部门流动)。这一部分我们主要估计一般均衡模型中的几个未知参数,用于在 Section 6 进行反事实模拟。
5.1 估计虚拟变量
第 (17) 式将双边贸易量同两国各自的特征以及地理信息联系了起来,对该式的估计使我们可以了解技术水平与地理障碍。
使用进口国的国内开支对 (17) 式的双边贸易数据进行标准化,令 \(\frac{X_{ni}}{X_n}\) 与 \(\frac{X_{nn}}{X_n}\) 相除可得
\[ \frac{X_{n i}}{X_{n n}}=\frac{\pi_{n i}}{\pi_{n n}}=\frac{T_{i}}{T_{n}}\left(\frac{w_{i}}{w_{n}}\right)^{-\theta \beta}\left(\frac{p_{i}}{p_{n}}\right)^{-\theta(1-\beta)} d_{n i}^{-\theta} \tag{25} \]
同样由 (17) 式可得
\[ \begin{aligned} \frac{X_{n n}}{X_{n}}&=\pi_{n n}=T_{n}\gamma^{-\theta}\left(\frac{w_{n}}{p_{n}}\right)^{-\beta\theta } \\ \frac{X_{i i}}{X_{i}}&=\pi_{i i}=T_{i}\gamma^{-\theta}\left(\frac{w_{i}}{p_{i}}\right)^{-\beta\theta } \end{aligned} \]
两式相除得
\[ \frac{p_{i}}{p_{n}}=\frac{w_{i}}{w_{n}}\left(\frac{T_{i}}{T_{n}}\right)^{-1 / \theta \beta}\left(\frac{X_{i} / X_{i i}}{X_{n} / X_{n n}}\right)^{-1 / \theta \beta} \]
代入 (25) 式消掉 \({p_i}/{p_n}\) 得到
\[ \ln \frac{X_{n i}}{X_{n n}}-\frac{1-\beta}{\beta}\ln \frac{X_{i} / X_{i i}}{X_{n} / X_{n n}}=-\theta \ln d_{n i}+\frac{1}{\beta} \ln \frac{T_{i}}{T_{n}}-\theta \ln \frac{w_{i}}{w_{n}} \]
为了化简该式,定义
\[\ln X_{n i}^{\prime} \equiv \ln X_{ni}-[(1-\beta)/\beta] \ln (X_i/X_{ii})\]
则有
\[ \ln \frac{X_{n i}^{\prime}}{X_{n n}^{\prime}}=-\theta \ln d_{n i}+\frac{1}{\beta} \ln \frac{T_{i}}{T_{n}}-\theta \ln \frac{w_{i}}{w_{n}} \tag{26} \]
进一步化简,定义
\[ S_i \equiv \frac{1}{\beta} \ln T_i - \theta \ln w_i \tag{27} \]
则有
\[ \ln \frac{X_{n i}^{\prime}}{X_{n n}^{\prime}}=-\theta \ln d_{n i}+S_i-S_n \tag{28} \]
其中,\(S_i\) 可以视为 \(i\) 国的竞争力(与技术正相关,与工资负相关),(28) 式就是我们要估计的基本方程18。
- 利用双边贸易数据,并取 \(\beta\) 的平均值 0.21,就可以计算 (28) 式的左边。
- 至于等式右边,\(S_i\) 是 \(i\) 国作为出口国时虚拟变量的系数(coefficients on source-country dummy),同样 \(S_n\) 是 \(n\) 国作为出口国时虚拟变量的系数。
- 最后则是贸易障碍 \(d_{ni}\),根据引力方程的相关文献,我们用一系列代理变量来表示它,包括距离、语言和贸易协定。\(\forall i \neq n\),建立回归模型:
\[ \ln d_{n i}=d_{k}+b+l+e_{h}+m_{n}+\varepsilon_{n i} \tag{29} \]
其中 \(d_k\) 表征六档离散距离的效应,\(b\) 表征共同边界,\(l\) 表征共同语言,\(e_h\) 表征是否共同存在于一个区域贸易协定中,\(m_n\) 表征 \(n\) 国作为进口国的目的地国效应(衡量目的地市场的开放程度)。
由于贸易的性质,需要对误差形式进行特别设定。设 \(\varepsilon_{ni}=\varepsilon_{ni}^1+\varepsilon_{ni}^2\),两部分之间不相关
这是因为,贸易具有互惠性,如果 \(i\) 国向 \(n\) 国出口的贸易障碍偏低(实际值低于模型拟合值),则一般 \(n\) 国向 \(i\) 国出口的贸易障碍也会偏低。这两个误差 \(\varepsilon_{ni}\) 和 \(\varepsilon_{in}\) 往往同时偏高或偏低,有一定相关性,故 \(\text{cov}(\varepsilon_{ni}, \varepsilon_{in})>0\),违反了 OLS 的基本假设 \(\text{cov}(\varepsilon_j, \varepsilon_k)= 0, \forall j \neq k\)
第一部分 \(\varepsilon_{ni}^1\) 符合 OLS 的经典假设,即 \(\begin{aligned}E(\varepsilon_{ab}^1\varepsilon_{cd}^1) = \left\{\begin{matrix} \sigma_1^2, & \forall a=c \land b=d\\ 0, & \text{otherwise.} \end{matrix}\right.\end{aligned}\)
第二部分专门体现两国贸易的互惠性,有性质 \(\varepsilon_{ni}^2=\varepsilon_{in}^2\),使得 \(E(\varepsilon_{ni}^2\varepsilon_{in}^2)= E(\varepsilon_{ni}^2\varepsilon_{ni}^2) =\sigma_2^2\)
则总误差满足
\[ \begin{aligned} E(\varepsilon_{ab}\varepsilon_{cd}) & = E(\varepsilon_{ab}^1\varepsilon_{cd}^1)+E(\varepsilon_{ab}^1\varepsilon_{cd}^2)+E(\varepsilon_{ab}^2\varepsilon_{cd}^1)+E(\varepsilon_{ab}^2\varepsilon_{cd}^2) \\ & = E(\varepsilon_{ab}^1\varepsilon_{cd}^1)+E(\varepsilon_{ab}^2\varepsilon_{cd}^2) \\ & = \left\{\begin{matrix}\sigma_1^2+\sigma_2^2, & \forall a = c \land b = d \\ \sigma_2^2, & \forall a = d \land b = c\\ 0, & \text{otherwise.} \end{matrix}\right. \end{aligned} \] 将 (29) 式代入 (28) 式得到
\[ \ln \frac{X_{n i}^{\prime}}{X_{n n}^{\prime}}=S_{i}-S_{n}-\theta m_{n}-\theta d_{k}-\theta b-\theta l-\theta e_{h}+\theta \varepsilon_{n i}^{1}+\theta \varepsilon_{n i}^{2} \tag{30} \]
利用 GLS (generalized least squares) 估计该模型,估计结果如 Table 3.
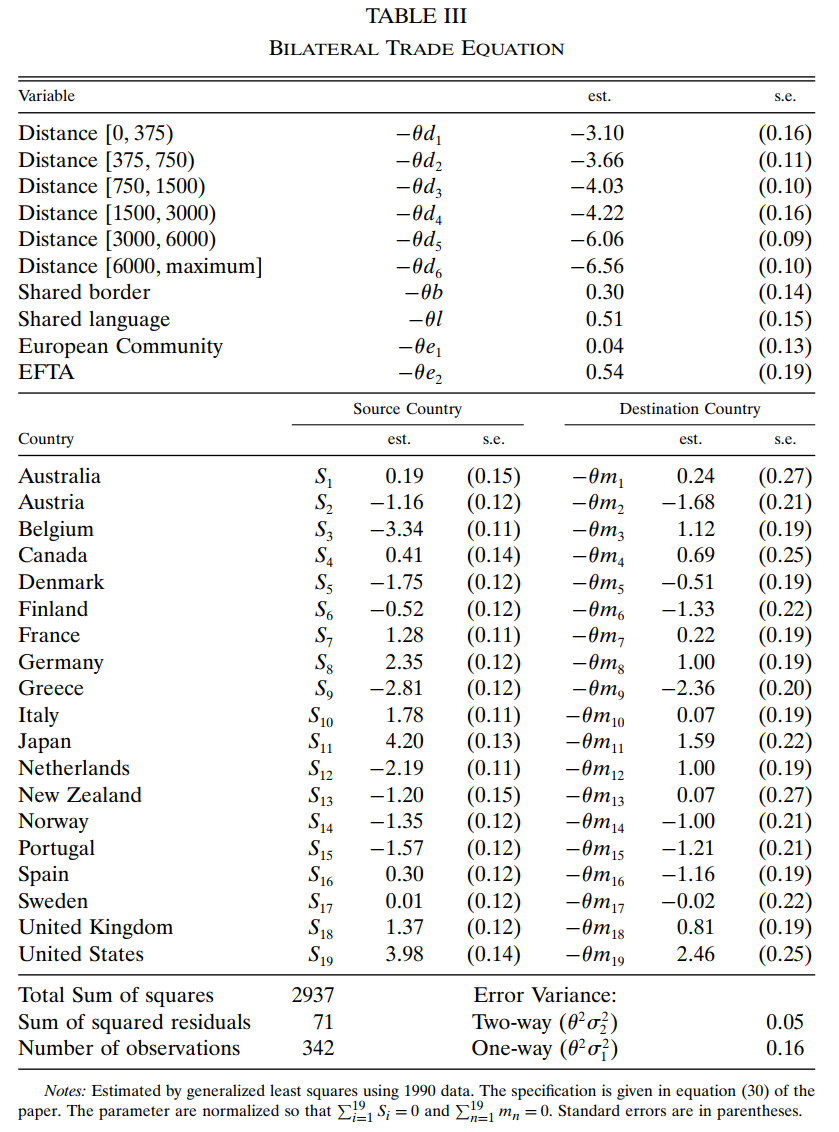
估计结果:
- \(S_i\) 的估计值表明,1990 年这 19 个 OECD 国家中,日本的竞争力最强,紧随其后的是美国。比利时和希腊是竞争力最差的
- 地理障碍的增加极大地阻碍贸易。共同语言则一定程度上有利于双边贸易。共同边界、欧共体和 EFTA 则不是很重要
EFTA 的系数比共同语言还大,为什么不重要?此处是否写错了?
- \(m_i\) 的估计值表明美国、日本和比利时是(市场)最开放的国家,希腊则是最封闭的
- \(\varepsilon_{ni}^2\) 的方差占误差方差的四分之一左右(two-way error variance 是它与 one-way error variance 总和的四分之一,计算过程见程序部分)
接下来我们用不同于 Section 3 的另外两种方法估计 \(\theta\).
5.2 利用工资数据估计 \(\theta\)
利用 (27) 式,以上文中估计出来的 \(S_i\) 作为被解释变量,用以下模型估计 \(\theta\)
\[ S_{i}=\alpha_{0}+\alpha_{R} \ln R_{i}-\alpha_{H}\left(\frac{1}{H_{i}}\right)-\theta \ln w_{i}+\tau_{i} \]
其中,\(R_i\) 为一国的 R&D 存量,\(H_i\) 为平均受教育年限,\(w_i\) 为经过教育调整的工资,\(\tau_i\) 为误差,\(\theta\) 为工资的系数。
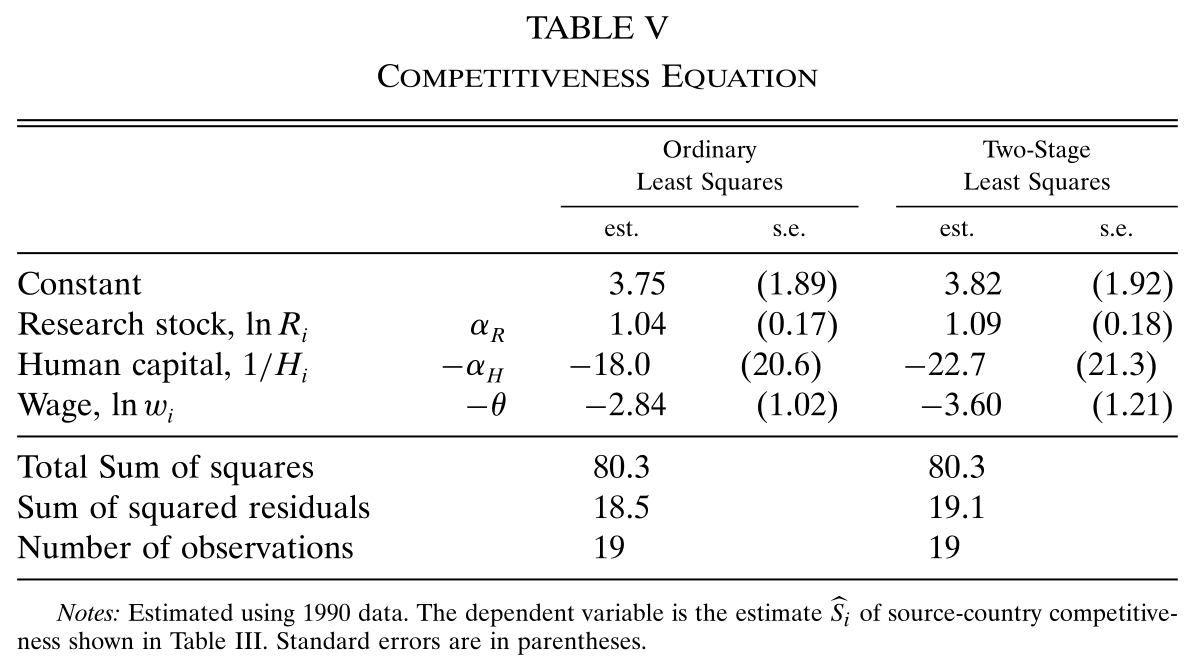
如 Table 5 的第三列显示,IV 估计出的 \(\theta\) 为 3.60,比 Section 3.2 的估计值略小。
但该模型的观测值只有19个,样本量太小了。
5.3 利用价格数据估计 \(\theta\)
估计一个结果被报告在正文中、但方程从未出现过的计量模型19:以 \(\ln (X'_{ni}/X'_{nn})\) 为被解释变量,\(D_{ni}\) 为内生解释变量,source & destination dummies 为外生解释变量,IV 估计值为 12.86
以下我们优先使用 3.2 节的估计值,因为它处于另外两种估计值之间。
5.4 估计技术水平和贸易障碍
5.4.1 估计技术
有了 \(\theta\) 的估计值,就可以根据 (27) 式将 \(T_i\)(第 2-4 列)从 \(S_i\)(第1列)中剥离出来,如 Table 6 所示。
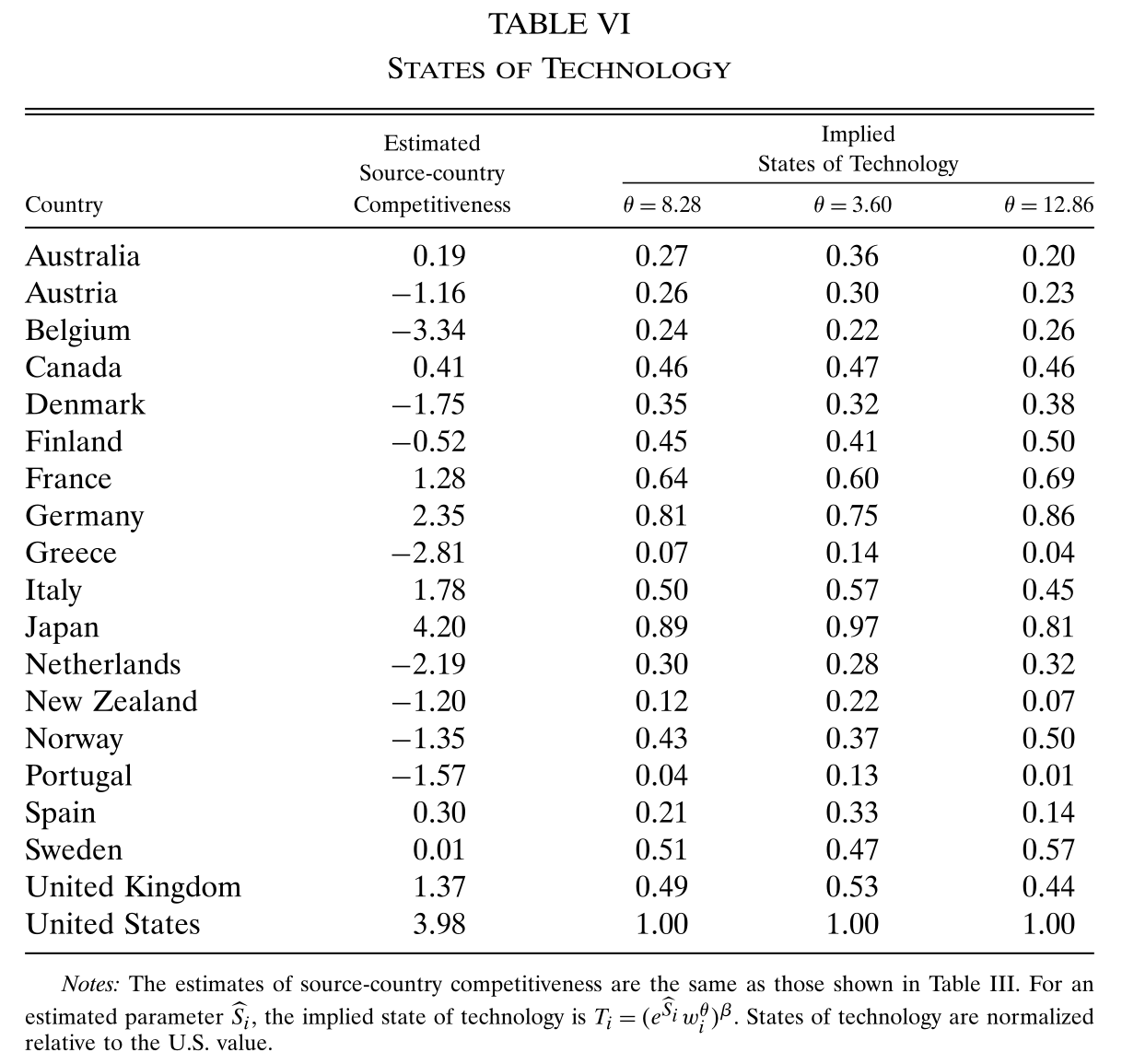
日本的竞争力虽然比美国强,但技术水平并不如美国,说明日本相对于美国的优势是由较低的工资造成的。另一方面,比利时的竞争力最低,但技术水平并不是最低,表明其竞争力受到了高工资的拖累。
5.4.2 估计贸易障碍
Table 3 中估计出来的各变量,都包含 \(-\theta\),将它们除以 \(-\theta\) 再以 \(e\) 为底数指数化后,即为 \(d_{ni}\) 中的一个因子。
由于 \(d_{ni}\) 为进口品到岸价格在离岸价格基础上的加成系数,所以上面得到的因子反映了该变量对进口品成本的影响。减 1 再乘 100% 后即为 Table 7 后三列的数字。
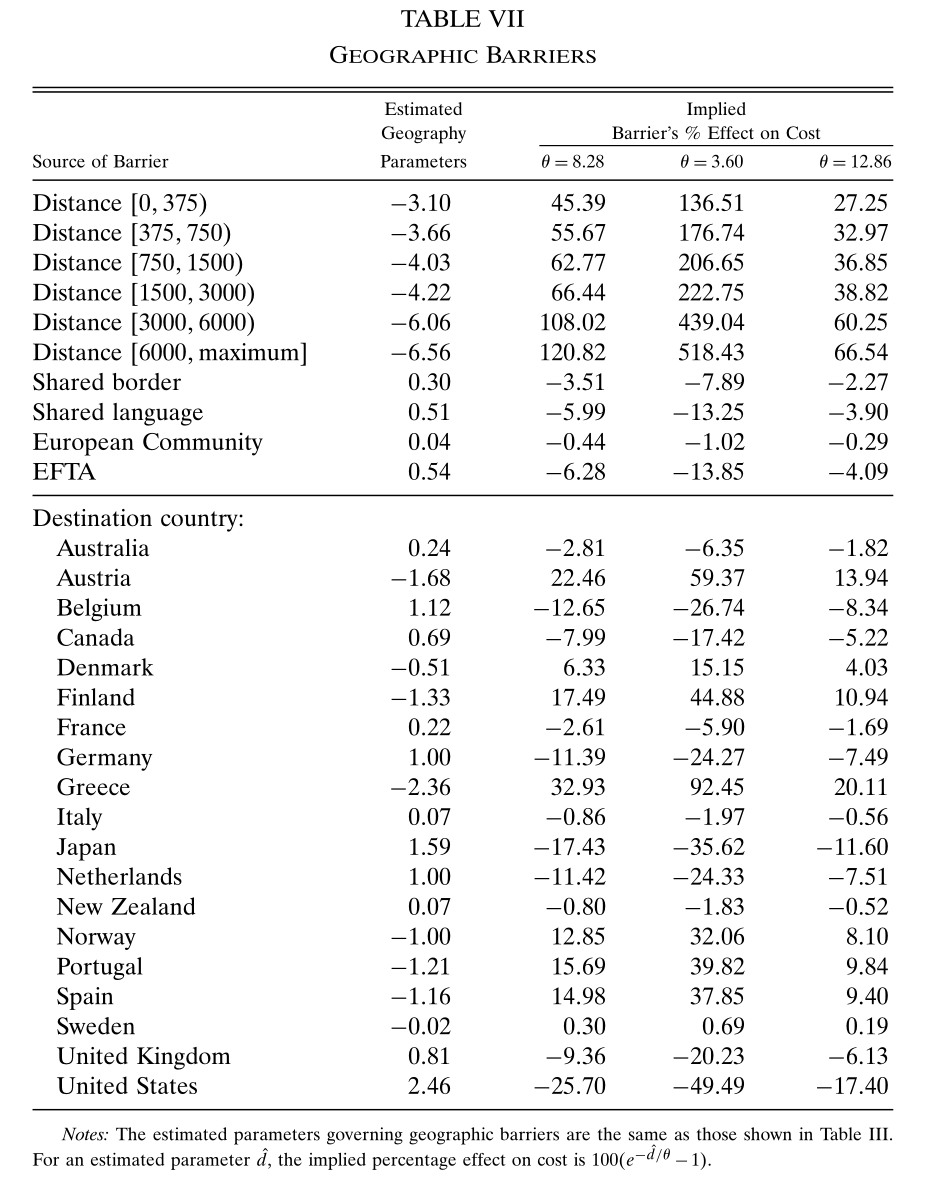
以共同语言为例,\(-\theta l\) 的估计值为 0.51. 若 \(\theta\) 取 8.28,则 \(e^l\) 为 0.94,表明拥有共同语言将使进口品的价格成为没有共同语言时的 0.94,从而价格的百分比变化为 \((0.94-1)\times 100\%=-5.97\%\)。