2 不完备模型6

仿照 Dornbusch et al. (1977)，设 \(i\) 国生产 \(j\in[0,1]\) 产品的效率为 \(z_i(j)\)。但 Dornbusch et al. (1977) 中只有一种生产要素——劳动，生产效率表示一单位劳动投入对应的产量；而本文中有两种生产要素，生产效率必须重新解释。

将制造业两种主要生产要素划分为劳动 \(L\) 和中间品 \(K\)，生产所需投入就是这两种要素的混合。假设：（1）一国内部要素市场均衡时，劳动和中间品的价格处处相同；（2）劳动和中间品在要素报酬中获取的份额恒定。

这个假设意味着，所有产品的生产函数不仅都是 C-D 式的，而且指数参数全部相同，即 \(y_i(j)=A_i(j)L^\beta K^{1-\beta}\)，产品的差别仅体现在技术上。根据要素价格可知劳动和中间品投入的比例，将一定量劳动与对应中间品的混合称为单位投入，其产量就是生产效率 \(z_i(j)\).

给定一国的要素价格，则其国内不同产业单位投入的成本是相同的。设 \(i\) 国单位投入的成本为 \(c_i\)，于是 \(i\) 国生产一单位 \(j\) 产品的成本是 \({c_i}/{z_i(j)}\)7.

通过设定冰山型成本引入地理障碍。设 \(i\) 国向 \(n\) 国出口商品，\(n\) 国每接收 1 单位产品到岸，需要 \(i\) 国离岸出口 \(d_{ni}\) 单位产品。因此地理障碍意味着

\[ \left\{\begin{array}{c}{d_{i i}=1} \\ {d_{n i}>1, \forall n \neq i}\end{array}\right. \]

于是 \(i\) 国生产的 \(j\) 产品在 \(n\) 国的价格为

\[ p_{ni}(j)=\frac {c_i}{z_i(j)} d_{ni} \tag{1} \]

\(n\) 国则在全世界范围内挑选最低价，假定完全竞争8 ，\(j\) 产品在 \(n\) 国的最终价格为（\(N\) 为国家总数）：

\[ p_{n}(j)=\min \left\{p_{n i}(j) ; i=1, \cdots, N\right\} \tag{2} \]

此外，设各国的效用函数相同，为 CES 型：

\[ U=\left[\int_{0}^{1} Q(j)^{(\sigma-1) / \sigma} d j\right]^{\sigma /(\sigma-1)} \tag{3} \]

替代弹性 \(\sigma>0\)

2.1 技术

设一国生产所有产品的效率服从该国特定的概率分布（所有产品独立同分布）：\(i\) 国生产所有产品的效率为一个随机变量 \(Z_i\)，其分布函数为 \(F_i(z) \equiv Pr[Z_i \le z]\)。根据大数定律，\(F_i(z)\) 也是 \(i\) 国生产的所有产品中，效率低于 \(z\) 的产品的比例。

由 (1) 式知，\(i\) 国生产的任一产品在 \(n\) 国的价格服从同一个分布，都可以用随机变量 \(P_{n i}=c_{i} d_{n i} / Z_{i}\) 来表示，从而 \(n\) 国最终消费的某种商品的价格为随机变量 \(P_{n}=\min \left\{P_{n i} ; i=1, \cdots, N\right\}\)。

此外，定义 \(i\) 国向 \(n\) 国提供某种商品的概率为 \(\pi_{n i}\)。

要获得形式比较简单的价格分布函数 \(P_{ni}\) 和 \(\pi_{n i}\)，需要对 \(F_i(z)\) 进行特殊设定。

设 \(F_i(z)\) 服从 Fréchet 分布9且各国的分布相互独立：

\[ F_{i}(z)=e^{-T_{i} z^{-\theta}} \tag{4} \]

其中，\(T_i>0, \theta >1\).

注意：\(\theta\) 参数对各国相同，是 transnational 的。

该分布有性质：(1) \(Z_i\) 的几何均值为 \(e^{\gamma/\theta}T_i^{1/\theta}\)（\(\gamma\)为欧拉常数），其对数的标准差为 \(\pi/(\theta \sqrt{6})\)；(2) 在 \(\theta\) 相同的前提下，\(T_i\) 反映各国的技术水平，该值越大，\(i\) 国企业以高效率生产的概率越大。因此 \(T_i\) 是某国生产率绝对优势的体现；(3) \(\theta\) 代表效率分布的离散程度，该值越小，分布越分散，各国之间克服地理障碍进行贸易的可能性越大。因此，\(\theta\) 是各国间潜在比较优势的体现。

如上图，为 \(Z_i\) 分布的概率密度函数，可以很直观地验证 (2)(3) 两条性质。

2.1.1 \(\theta\) 的经济含义

为什么说 Fréchet 分布的技术异质化程度参数 \(\theta\) 可以表征比较优势的大小？因为

  1. EK2002 的 (12) 式表明，\(\theta\) 越小，贸易障碍对标准化贸易份额的负面影响越小，即贸易克服贸易障碍的能力越强。
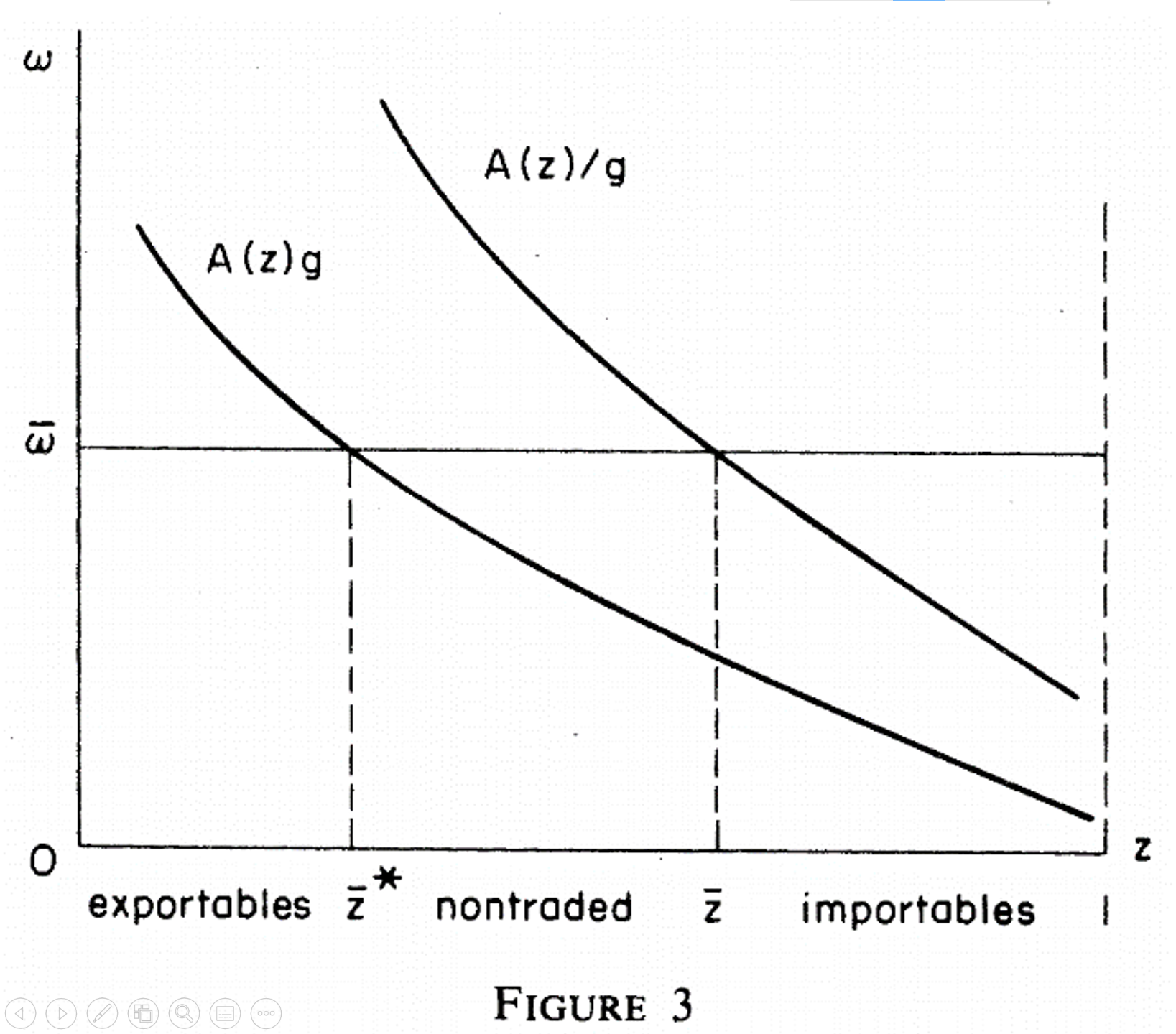
  2. 而在 DFS1977 中，比较优势（两国相对生产率跨产业的异质化程度） \(CA\) 越大，\(A(z)\) 越陡峭10（注意，这个 \(z\) 是产品的编号，与 EK2002 中表示效率的 \(z\) 不同），贸易的冰山成本 \(g\) 对可贸易品范围的负面影响越小 (Section 3.B)，即贸易克服冰山成本的能力越强。

\[ CA(i,j) \equiv \frac{a(i)/a(j)}{a^\ast(i)/a^\ast(j)}=\frac{a(i)}{a^\ast(i)}\frac{a^\ast(j)}{a(j)}=\frac{A(j)}{A(i)} \]

EK2002 与 DFS1977 相比，内在机制虽不尽相同，但这两个结论在结构上是很相似的，因此我们可以将 \(\theta\) 称为比较优势参数11。

但不容易在几何上找到对 \(\theta\) 的直观解释，这与 DFS1977 不同。

从几何直观来看，\(\theta\) 意味着一国产业效率的异质化程度。

\(\theta \rightarrow \infty\) 时，Fréchet 分布的概率密度函数在 \(z=1\) 处塌缩为一个高度为无穷大的尖峰，意味着一国所有产业的效率相同，价格也相同。用 DFS1977 的观点看，则 \(\begin{aligned} \frac{A(j)}{A(i)}=\frac{a(i)/a(j)}{a^\ast(i)/a^\ast(j)}=\frac{1}{1}=1 \end{aligned}\)，\(A(z)\) 曲线是平的，若有贸易障碍，会吞噬所有的可贸易品范围。

\(\theta \rightarrow 0\) 时，Fréchet 分布的概率密度函数是一条高度非常低的双曲线，每个国家的生产效率都有广泛的分布。在大数定律下，对于任一产品门类，两国的生产效率之比 \(a^\ast(j)/a(j)=A(j)\) 可以从接近零变异到无穷大。用 DFS1977 的观点看， \(A(z)\) 的变化从最低的接近零变化到最高的趋于无穷大，非常陡峭，则贸易克服贸易障碍的能力会非常强。

2.2 价格

2.2.1 价格分布

首先求 \(P_{ni}\) 的分布，定义其分布函数为

\[ G_{ni}(p) \equiv Pr[P_{ni} \le p] \]

则有：

\[ G_{ni}(p) =1-e^{-T_{i} ( {{c_i}d_{ni}})^{-\theta}p^{\theta}} \tag{5} \]

证明： \[ \begin{aligned} G_{ni}(p) & \equiv Pr[P_{ni} \le p] \\ &= Pr[\frac {{c_i}d_{ni}}{Z_i} \le p] = Pr[Z_i \geq \frac {{c_i}d_{ni}}{p}] \\ & = 1-Pr[Z_i \le \frac {{c_i}d_{ni}}{p}] = 1 - F_i(\frac {{c_i}d_{ni}}{p}) \\ &= 1 - e^{-T_{i} (\frac {{c_i}d_{ni}}{p})^{-\theta}} = 1-e^{-T_{i} ( {{c_i}d_{ni}})^{-\theta}p^{\theta}} \quad \blacksquare \end{aligned} \]

这是 \(i\) 国出口到 \(n\) 国的某种产品价格小于等于 \(p\) 的概率，经过市场竞争，最终 \(n\) 国该种产品的价格小于等于 \(p\) 的概率为

\[ G_n(p) =1-\prod_{i}{(1-G_{ni}\left(p\right))} \]

证明：\[\begin{aligned} G_n(p) &= Pr[P_n \le p] \\ &=Pr[ \min \left\{P_{n i} ; i=1, \cdots, N\right\} \le p] \\ &= 1 - Pr[ \min \left\{P_{n i} ; i=1, \cdots, N\right\} \geq p] \\ &= 1- Pr[ P_{n i} \geq p; i=1, \cdots, N]\\ &=1-\prod_{i}Pr\left\{P_{ni}\geq p\right\} \\ &=1-\prod_{i}{(1-G_{ni}\left(p\right))} \quad \blacksquare \end{aligned}\]

将 (5) 式代入，得

\[ G_n\left(p\right)=1-e^{-[\sum_{i=1}^{N}T_{i} ( {{c_i}d_{ni}})^{-\theta}]p^{\theta}} \]

将其记为

\[ G_{n}(p)=1-e^{-\Phi_{n} p^{\theta}} \tag{6} \]

其中，定义价格参数

\[ \Phi_{n} = \sum_{i=1}^{N}T_{i} ( {{c_i}d_{ni}})^{-\theta} \tag{7} \]

价格参数 \(\Phi_n\) 非常重要，因为它包含了影响各国价格的3个因素：（1）技术水平 \(T_i\)；（2）要素成本 \(c_i\)；（3）地理障碍 \(d_{ni}\)。

2.2.2 \(\Phi_n\) 的性质

  1. 国家数量越多，或国家数量不变而 \(T_i\) 越大，都会使 \(\Phi_n\) 越大，从而 \(G_{n}(p)\) 越大，即价格的期望会越小。因此，更广泛的国际贸易可以使本国居民享受到更低的价格水平，就像各国技术提高了一样。
  2. 国际贸易的利得会受到要素成本和地理障碍的削弱。考虑两种极端情况：
    1. 零障碍，即 \(d_{n i} \equiv 1, \forall n, i\)，此时 \(\Phi_{n} = \sum_{i=1}^{N}T_{i}{c_i}^{-\theta}\) 对于所有国家都一样，从而各国价格的分布函数一致。这就是概率版本的一价定律：各国价格的概率分布完全相同（但具体到某种产品，实际价格通常不同）
    2. 自给自足，即 \(d_{n i} \rightarrow \infty, \forall n \neq i\)，此时 \(\Phi_{n} = T_{n}{c_n}^{-\theta}\)，价格只受本国技术和要素成本影响。

2.2.3 价格分布的三个性质

2.2.3.1 性质1

\(n\) 国最终选择从 \(i\) 国购买某种产品 \(j\) 的概率为

\[ \pi_{n i}=\frac{T_{i}\left(c_{i} d_{n i}\right)^{-\theta}}{\Phi_{n}} \tag{8} \]

证明：
由于独立同分布，\(N\) 维空间中的联合概率密度函数可以表示为 \(N\) 个概率密度函数的积\[\begin{aligned} \pi_{n i}&=\operatorname{Pr}\left[P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right] \\ &=\int\cdots\int_{\left[P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right]}{ f(p_{n 1}, \cdots ,p_{n n}) d p_{n 1} \cdots d p_{n n}}\\ &=\int\cdots\int_{\left[P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right]}{ \prod_{i=1}^{N}f_{ni}(p_{ni})d p_{n 1} \cdots d p_{n n}}\\ &={\int_{0}^{\infty} f_{n i}(p_{ni})\left[\prod_{s \neq i} \int_{p_{ni}}^{\infty}f_{n s}(p_{ns}) d p_{n s}\right] d p_{ni}}\\ &={\int_{0}^{\infty} f_{n i}(p_{ni})\prod_{s \neq i} \left [1 - G_{n s}(p_{ni})\right] dp_{ni}} \\ &=\int_{0}^{\infty} \prod_{s \neq i}\left[1-G_{n s}(p_{ni})\right] d G_{ni}(p_{ni}) \\ &=\int_{0}^{\infty} \prod_{s \neq i}e^{ -T_{s}\left(c_{s} d_{n s}\right)^{-\theta} p_{ni}^{\theta}} \cdot e^{ -T_{i}\left(c_{i} d_{n i}\right)^{-\theta} p_{ni}^{\theta}} T_{i}\left(c_{i} d_{n i}\right)^{-\theta} d p_{ni}^{\theta}\\ &=T_{i}\left(c_{i} d_{n i}\right)^{-\theta}\int_{0}^{\infty} e^{ -\Phi_n p_{ni}^{\theta}} d p_{ni}^{\theta}\\ &=\frac{T_{i}\left(c_{i} d_{n i}\right)^{-\theta}}{\Phi_{n}} \quad \blacksquare \end{aligned}\]

同时，\(\pi_{ni}\) 也是 \(\Phi_{n}\) 中 \(i\) 国的贡献比例。

由无限种商品连续统的假设，结合大数定律知，\(n\) 国最终从 \(i\) 国购买的产品种类占 \(n\) 国消费全部产品种类的比例也是 \(\pi_{ni}\).

2.2.3.2 性质2

\(n\) 国最终选择从 \(i\) 国购买某种产品，其价格的条件概率分布也是 \(G_{n}(p)\)。

证明： \[ \begin{aligned} & \operatorname{Pr}\left[ P_{n i} \leq p \mid P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right] \\ =& \frac{\operatorname{Pr}\left[P_{n i} \leq p, P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right]}{\operatorname{Pr}\left[P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right]}\\ =& \frac{\int \cdots \int_{\left[P_{n i} \leq p, P_{n i} \leq \min \left\{P_{n s}; s \neq i\right\}\right]} \prod_{i = 1}^{N} f_{n i}\left(p_{n i}\right) d p_{n 1} \ldots d p_{n n}}{\pi_{n i}}\\ =& \frac{\int_{0}^{p} f_{n i}\left(p_{n i}\right)\left[\prod_{s \neq i} \int_{p_{n i}}^{\infty} f_{n s}\left(p_{n s}\right) d p_{n s}\right] d p_{n i}}{\pi_{n i}}\\ =& \frac{\int_{0}^{p} f_{n i}\left(p_{n i}\right) \prod_{s \neq i}\left[1-G_{n s}\left(p_{n i}\right)\right] d p_{n i}}{\pi_{n i}}\\ =& \frac{\int_{0}^{p} \prod_{s \neq i}\left[1-G_{n s}\left(p_{n i}\right)\right] d G_{n i}\left(p_{n i}\right)}{\pi_{n i}}\\ =& \frac{\left[T_{i}\left(c_{i} d_{n i}\right)^{-\theta}\right]\int_{0}^{p} e^{-\Phi_{n} p_{n i}^{\theta}} d p_{n i}^{\theta}}{\pi_{n i}}\\ =& 1-e^{-\Phi_{n} p^{\theta}} \\ =& G_n(p) \quad \blacksquare \end{aligned}\]

由大数定律知，最终 \(n\) 国从 \(i\) 国进口的所有产品的价格分布也是 \(G_{n}(p)\)。因此，不同来源国产品价格的概率分布一致。

如何理解这条性质呢？由 (11) 式知，技术水平高、投入成本低、到 \(n\) 国地理障碍少的国家，以所有产品计算，到达 \(n\) 国的商品到岸价格的均值会更低。但事实上，\(n\) 国只会购买该国生产最有效率的一部分产品。而对于缺乏竞争优势的国家，虽然以所有产品计算，到达 \(n\) 国的商品到岸价格的均值会高一些，但 \(n\) 国购买其产品更少，集中在其最有竞争力的商品上。最终，A source with a higher state of technology, lower input cost, or lower barriers exploits its advantage by selling a wider range of goods, exactly to the point at which the distribution of prices for what it sells in \(n\) is the same as \(n\)’s overall price distribution. 两国在 \(n\) 国出售商品的价格分布刚好一致。

比如，德国技术水平高，在许多产品中具有价格优势；西班牙技术水平低，具有价格优势的产品品种就比较少。但是，如果本国购买更多种类的德国产品，而只买很少数量的西班牙最有竞争力的产品，则最终对两国产品的平均购买价格可能是一样的。

2.2.3.3 性质3

在 \(\sigma < 1 + \theta\) 的前提下12，CES 效用函数对应的价格指数13

\[ p_{n}=\gamma \Phi_{n}^{-1 / \theta} \tag{9} \]

其中 \(\gamma=\left[\Gamma\left(\frac{\theta+1-\sigma}{\theta}\right)\right]^{1 /(1-\sigma)}\).

因各国的 \(\Phi_{n}\) 受到地理障碍的影响而不同，故各国的价格指数不同。因此，地理障碍这个因素使各国价格偏离一价定律，且越远离其他国家的国家，其价格指数越大。

证明：
\(n\) 国价格指数为 \(p_n=\left[\int_0^1 p_n(j)^{1-\sigma}dj\right]^{\frac{1}{1-\sigma}}\). 方括号中的统计量实际上是对商品连续统的一个积分，可以将其写成面积和的形式：将 \([0,1]\) 区间划分为 \(S\) 份，计算每份的面积：\(\int_0^1 p_n(j)^{1-\sigma}dj=\lim_{S \to \infty} \sum_{k=1}^{S} \left[\frac{1}{S}\cdot p_{n}(k)^{1-\sigma}\right]\) 由于 \(p_n(k)\sim G_n(p)\) 独立同分布，上式中的面积和可以视为同一个随机变量 \((P_n)^{1-\sigma}\) 多次抽样的均值 \(\frac{1}{S}\cdot\sum_{k=1}^{S} p_{n}(k)^{1-\sigma}\)。当抽样次数趋于无穷大时，根据大数定律，该均值等于 \((P_n)^{1-\sigma}\) 的期望。则 \[\begin{aligned} \int_0^1 p_n(j)^{1-\sigma}dj & = E\left[P_n^{1-\sigma}\right] = \int_{0}^{\infty}p^{1-\sigma}f_n(p)dp \\ &= \int_{0}^{\infty}p^{1-\sigma}dG_n(p)=\int_{0}^{\infty }p^{1-\sigma}e^{-\Phi_n p^\theta} d(\Phi_n p^\theta) \\ & \stackrel{\text{令 }x=\Phi_n p^{\theta}}{=} \int_{0}^{\infty}\left(x/\Phi_n\right)^{\frac{1-\sigma}{\theta}}e^{-x}dx \\ &= \Phi_n^{-\frac{1-\sigma}{\theta}}\int_{0}^{\infty }x^{\frac{1+\theta-\sigma}{\theta}-1}e^{-x}dx \\ &=\Phi_n^{-\frac{1-\sigma}{\theta}}\Gamma (\frac{1+\theta-\sigma}{\theta}) \end{aligned}\] 从而 \[ p_n=\Phi_n^{-\frac{1}{\theta}}\left[\Gamma (\frac{1+\theta-\sigma}{\theta})\right]^{\frac{1}{1-\sigma}}=\gamma \Phi_n^{-\frac{1}{\theta}} \quad \blacksquare \]

2.3 贸易流量和引力

由上一节价格分布的性质 2 知，\(n\) 国消费的每种产品的价格分布与来源地无关，均服从 \(G_n(p)\)。在连续统商品的假设下，\(n\) 国从每个国家都购买了无穷多种商品，则 \(n\) 国从每个国家购买的商品的平均价格都应严格等于 \(G_n(p)\) 这个分布所对应的期望，是相同的。因此 \(n\) 国从一个国家的进口支出与从该国进口的商品数量成正比。

又因为效用函数是对称的，在所有商品价格服从同一分布的前提下，其消费数量也服从同一分布。故由大数定律，从一国进口商品的数量与进口商品的种类成正比。因此，\(n\) 国从 \(i\) 国进口支出占 \(n\) 国制造业总支出的比例，就等于 \(n\) 国从 \(i\) 国进口商品种类占所有消费商品种类的比例，由性质 1 知，该比例为 \(\pi_{ni}\)，即：

\[ \frac{X_{n i}}{X_{n}}=\pi_{ni}=\frac{T_{i}\left(c_{i} d_{n i}\right)^{-\theta}}{\Phi_{n}}=\frac{T_{i}\left(c_{i} d_{n i}\right)^{-\theta}}{\sum_{k=1}^{N} T_{k}\left(c_{k} d_{n k}\right)^{-\theta}} \tag{10} \]

其中，\(X_{n}\) 为 \(n\) 国制造业总支出，\(X_{n i}\) 为 \(n\) 国自 \(i\) 国的制造业产品进口额。

\(i\) 国制造业的总收入为：

\[ Q_{i}=\sum_{m=1}^{N} X_{m i}=T_{i} c_{i}^{-\theta} \sum_{m=1}^{N} \frac{d_{m i}^{-\theta} X_{m}}{\Phi_{m}} \]

由此可得

\[ T_{i} c_{i}^{-\theta}=Q_i/\sum_{m=1}^{N} \frac{d_{m i}^{-\theta} X_{m}}{\Phi_{m}} \]

将其代入 (10) 式并结合 (9) 式得到

\[ X_{n i}=\frac{\left(\frac{d_{n i}}{p_{n}}\right)^{-\theta} X_{n}}{\sum_{m=1}^{N}\left(\frac{d_{m i}}{p_{m}}\right)^{-\theta} X_{m}} Q_{i} \tag{11} \]

我们推出的 (11) 式是一个标准的引力方程。它具有以下性质：（1）双边贸易额对 \(n\) 国制造业产品总支出 \(X_n\) 和 \(i\) 国制造业总收入 \(Q_i\) 的弹性为114。（2）地理障碍 \(d_{ni}\) 被进口国的价格指数 \(p_n\) 缩减。给定 \(i\) 国的总出口额 \(Q_i\)，可以将 (11) 式右边的分母视为 \(i\) 国眼中的全球市场，则分子与分母的比就是 \(n\) 国所占份额。\(p_n\) 的下降与地理障碍 \(d_{ni}\) 的上升具有相同的作用，即阻碍 \(i\) 国产品进入 \(n\) 国（地理障碍越大，进口国本国物价越便宜，出口国的商品越不容易进来）。

参考文献

Bernard AB, Eaton J, Jensen JB, Kortum S. Plants and productivity in international trade. American Economic Review. 2003;93.
Dornbusch R, Fischer S, Samuelson PA. Comparative advantage, trade, and payments in a ricardian model with a continuum of goods. The American Economic Review. JSTOR; 1977;67(5):823–39.

  1. A Model of Technology, Prices, and Trade Flows. 半个一般均衡模型：将要素价格作为外生变量。↩︎

  2. “单位投入”中所包含的要素数量可以是任意的，这不重要。因为要素投入得多/少，成本 \(c_i\) 和产量 \(z_i(j)\) 会同步增/减。产品价格（单位产品成本） \({c_i}/{z_i(j)}\) 才是真正关键的变量，而它不会因为”单位投入”设定的要素数量而变化。↩︎

  3. 此处的完全竞争假设可以拓展为 Bertrand 竞争，参见 Bernard et al. (2003).↩︎

  4. 又称 Type II extreme value distribution. 极值分布是从很多彼此独立的随机变量中挑出来的极大值（或者极小值）的概率分布。因 \(P_n\) 是取 \(N\) 个值中的极小值，故尝试了这种分布。↩︎

  5. 在 DFS1977 框架中，我们甚至可以给出一个比较优势的操作性定义，即 \(A(z)\) 的平均陡峭程度：\(CA_{simple} \equiv \frac{A(1)}{A(0)}\).↩︎

  6. 作者解释 \(\theta\) 的经济学含义时，在脚注 15 中引用了 DFS1977. 他用随机抽样方法构造了符合 Fréchet 分布的生产率数据样本，然后推导了 \(A(z)\) 与 \(T\) 的关系，表明两国的技术水平之比 \(T^\ast/T\) 越大，\(A(z)\) 越陡峭。所以除了 \(\theta\)，两国技术水平之比其实也是能够表征比较优势的参数。↩︎

  7. \(\Gamma\) 分布要求参数 \(\frac{1+\theta-\sigma}{\theta}>0\)，所以必须有 \(\sigma < 1 + \theta\).↩︎

  8. 第四部分中可以推导，对于 CES 效用函数，有价格指数 \(p=\left[\int_0^1 p(j)^{1-\sigma}dj\right]^{\frac{1}{1-\sigma}}\)，满足 \(U=I/p\)。因此，求出该价格指数对于计算效用是非常方便的。↩︎

  9. 前提是 \(N\) 充分大，或 \(n\) 国为一个小国。↩︎